Conception de nouveaux
Produits Manufacturés.
Introduction au tolérancement capable

On veut souvent restreindre la maitrise des performances d’un produit à la réduction des tolérances des paramètres fonctionnels pour limiter la dispersion des conditions d’aptitude à l’emploi. Ce phénomène est accentué par l’exigence de la CAO, qui a besoin au plus tôt, de nominaux pour pouvoir modéliser ce dernier dans l’espace.
Il faut en réalité sortir de ce paradigme et comprendre la relation Intervalle de Tolérance / Nominal des cotes avec les balises des Conditions fonctionnelles. Ceci est primordial pour maitriser sa conception, ses coûts et ses délais.
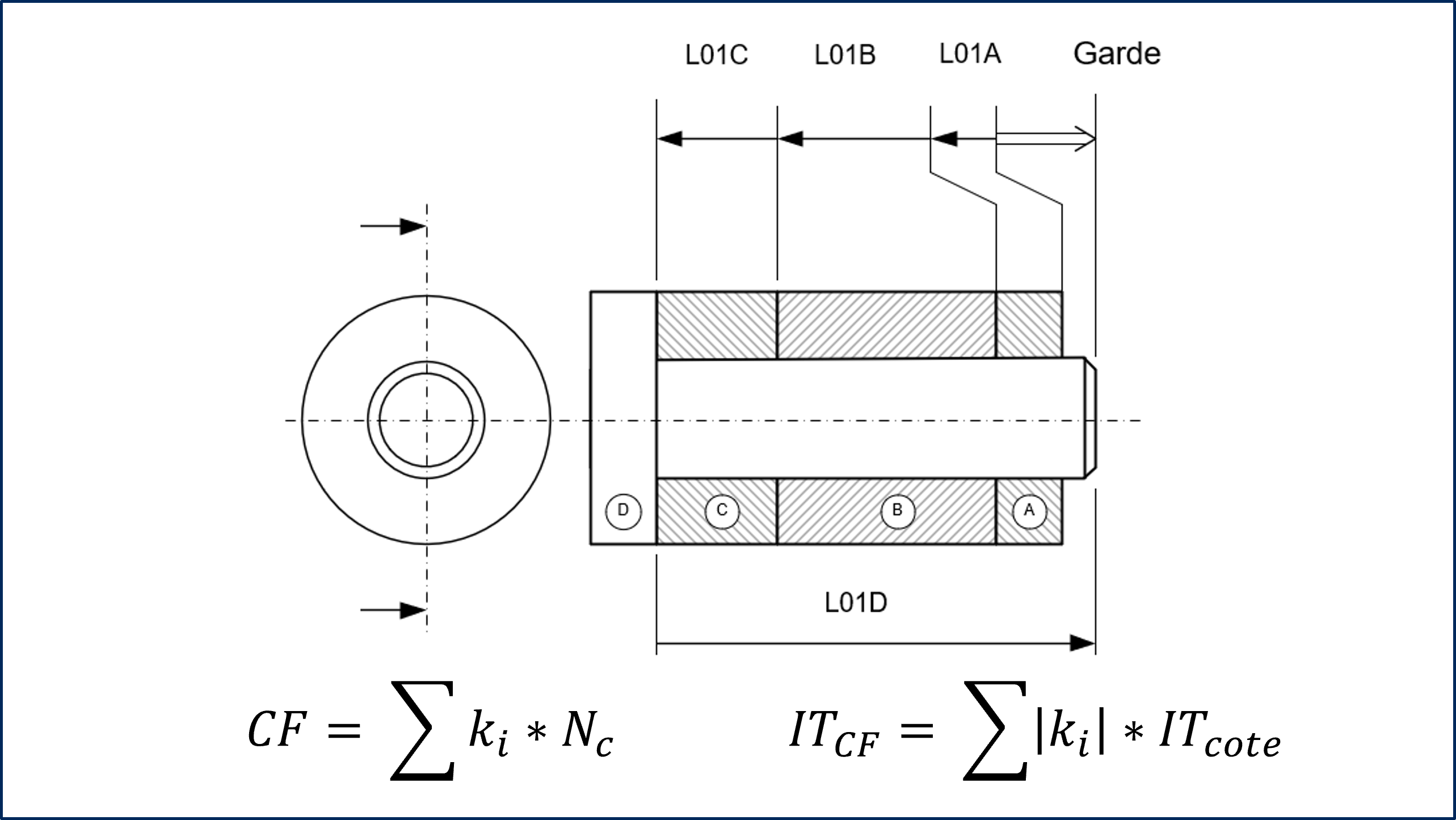
Prenons un exemple simple d’empilement de pièces sur un axe en pire cas appelé Garde.
La condition fonctionnelle se calcule comme une chaine de cotes vectorielle dans laquelle Ki représente la sensibilité ou la dérivée partielle (ΔL/L) du paramètre fonctionnel pour la condition.
La dispersion de l’assemblage est définie en linéaire comme étant la somme des intervalles de tolérance des paramètres fonctionnels.

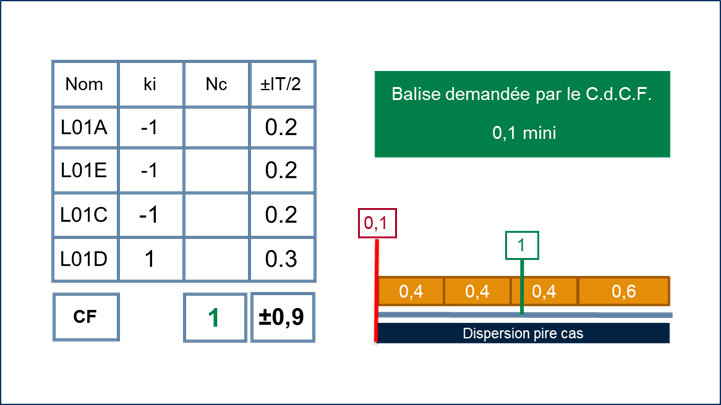
En absence de balises fonctionnelles, il est quand même possible de calculer la dispersion de la condition.
L’Intervalle de Tolérance est donc de 1.8 mm.
Le graphe représente donc l’étendue de l’intervalle de Tolérance (IT).
Pour diminuer cette dispersion, si vous n’utilisez pas les statistiques dans votre process de développement de qualification et de production, seule la réduction des IT est envisageable, ce qui aura comme conséquence l’augmentation du coût de la pièce.
A cette condition de dépassement est associé une exigence dimensionnelle définie par le cahier des charges fonctionnel (C.d.C.F.) qui garantit la performance de l’assemblage lorsque le dépassement est supérieur à 0.1mm.
Prenons donc en compte cette balise dans notre analyse.
La mise en place de cette balise uni-limite permet de déterminer la valeur cible (moyenne) minimum à atteindre pour respecter l’exigence du C.d.C.F.
Elle correspond à la balise mini plus la moitié de la tolérance de l’assemblage.
![]()
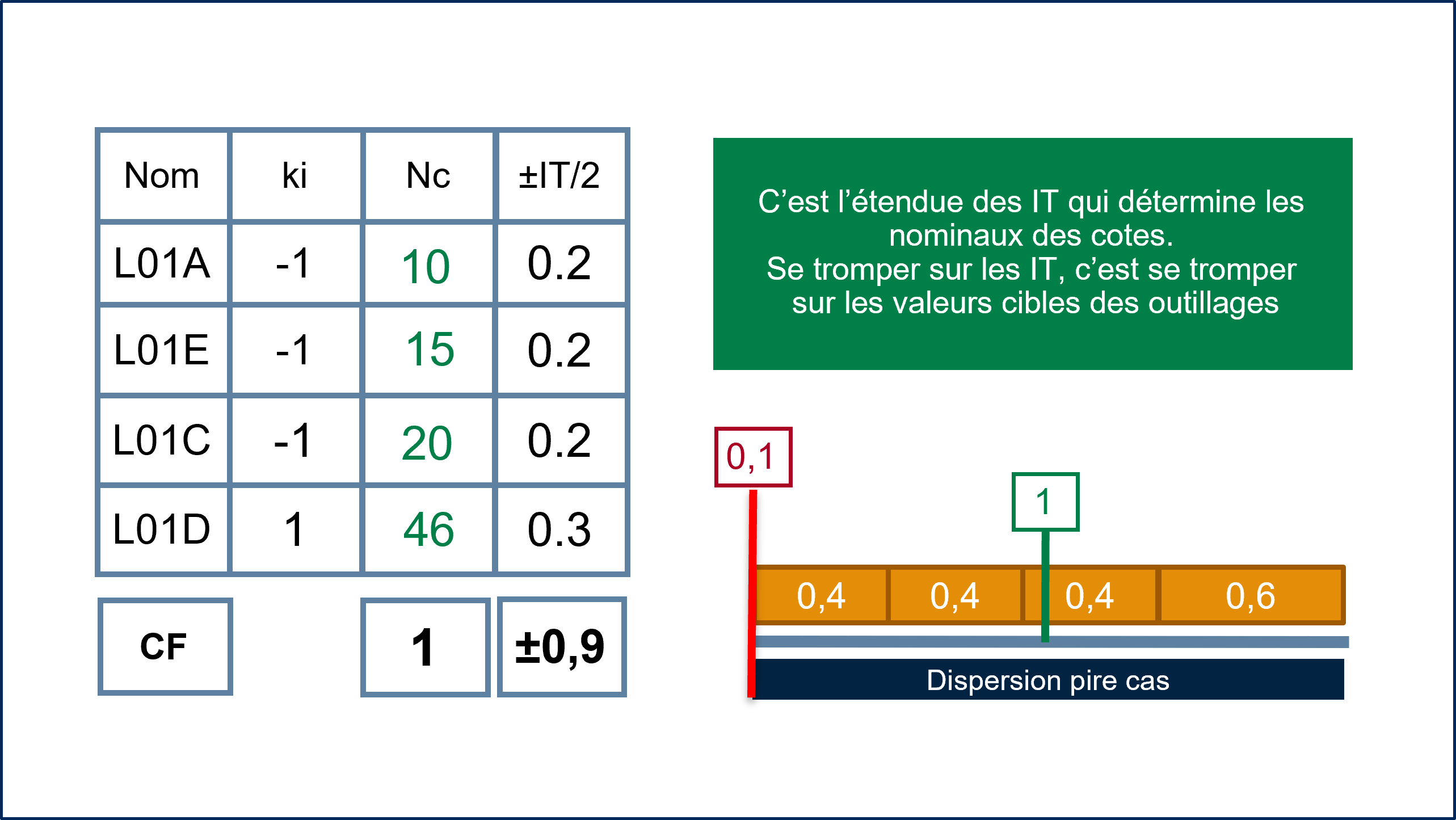
Ensuite il suffit de résoudre l’équation des nominaux afin de connaitre le Nominal Centré de chaque composant.
Cette valeur de nominal devient la cible :
- de l’outillage
- de production,
- d’une action 6sigma, qui sera bénéfique car la cible est connue.
Ne pas oublier que c’est l’étendue des IT qui détermine les nominaux des cotes. Dès que l’on se trompe sur les IT, on se trompe sur les valeurs cibles des outillages.
Et les implications de cette erreur seront fortes :
- Risque important de modifications successives,
- Plus de risques de non-conformités en production,
- Génération de surcoût non pris en compte dans le prix pièce,
L’augmentation des délais.
On comprend bien, grâce à cet exemple simple, que l’intervalle de tolérance et les capabilités de vos moyens de productions sont au centre du processus de développement d’un produit performant et fiable.
Pour se donner des garanties de faisabilité coût/délais, il faudra appliquer cette méthode sur des systèmes complexes, faisant intervenir de nombreuses exigences fonctionnelles, parfois contradictoires, qui interagissent et se télescopent, pressé par une exigence de mise sur le marché et de profitabilité forte. La réponse à ce défi passera par l’application d’une politique statistique et cohérente entre le bureau d’étude, les services industrialisation, outillage et la production.
Vous souhaitez en savoir plus ou faire appel à notre expertise dans la conception pour appliquer cette démarche sur vos produits ? n’hésitez plus et contactez-nous
Vous avez des doutes quant à la viabilité de cette démarche ? Vous souhaitez en apprendre plus sur les méthodes de qualification employés dans nos études et outils? N’hésitez pas à nous contacter.





